Green's functions and fundamental solutions

The fundamental solution is always related to a specific partial differential equation (PDE). For some equations, it is possible to find the fundamental solutions from relatively simple arguments that do not directly involve "distributions." One such example is Laplace's equation of the potential theory considered in Green's Essay.

Laplace's equation governs many important physical problems, e.g. electric and steady-state heat conduction, etc. The equation has the following form in the Cartesian coordinate system x, y, z.

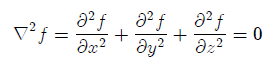
The function f that satisfies Laplace's equation is called a harmonic function.

Coor

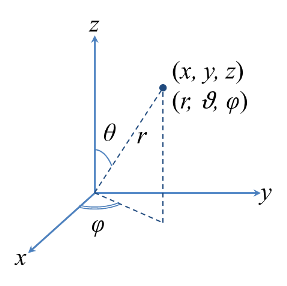
In the spherical coordinate system

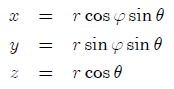
polar

Laplace's equation can be re-written as follows:

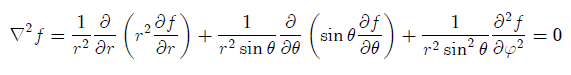
Let us now consider the problem of an unbounded space containing a point source (e.g. heat source) of unit strength. We can choose the coordinate system in such a way that its origin is located at the same point as one of the sources.

It is clear that the function f (e.g. temperature in steady-state heat conduction) is symmetric, as there is no reason for it to vary differently in the directions of different angles? and ?. This means that all the derivatives of function f with respect to those angles vanish, and the function satisfies the following ordinary differential equation

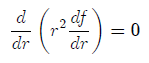
that has a following simple solution

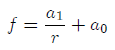
From the theory of ordinary differential equations, we know that the constants can be found from the additional boundary conditions. The space is unbounded, so the condition at infinity is one of those boundary conditions. The constant should be equal to zero if we are looking for the solution that vanishes at infinity. The function f should also satisfy the conservation law, which for potential problems means that the flux from the unit source must be equal to the total flux across any surface S that surrounds it.

Assuming that the surface S is a sphere with the radius ? one can mathematically formulate the law as

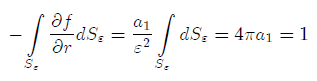
from which it follows that the constant should be equal to 1/(4?).

Thus, following relatively simple arguments, we obtained the fundamental solution, f = 1/(4? r), of the Laplace's equation that Green used in his Essay. Although we did not involve "distributions," the fundamental solution is not a regular function as it tends to infinity when r tends to zero. So, the fundamental solution is a singular function.

We assumed above that the origin of the Cartesian coordinate system coincided with the point source. By moving the origin to some point x'(x', y', z'), one can obtain a more general form of the fundamental solution

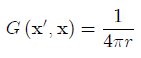
where the distance r between the point x'(x', y', z') of the applied source and the point x(x, y, z) is defined as follows

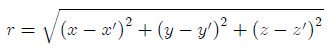
This solution satisfies the Laplace's equation everywhere except for the point x'.

The relative simplicity of the above procedure is the result of the symmetry of the problem. The same procedure can be used, for example, to obtain the fundamental solution of the Helmholtz equation that governs some wave propagation problems. The fundamental solution to that equation represents the field generated by a unit concentrated harmonic source. Unfortunately, similar problems for other partial differential equations may not possess spherical symmetry. For example, consider elasticity theory. To find the fundamental solution for Navier-Cauchy equations of elasticity one needs to solve the problem of an unbounded space containing a unit point load. The fields in elasticity problems (displacements and tractions) are vector fields, not scalar ones as those of the potential theory (potential and flux). The point load can be applied in different directions (e.g. in the directions of the axes x, y, z of a Cartesian coordinate system) and the displacements these loads produce would be different in different directions. This example demonstrates that, in general, the problem of finding fundamental solutions may be difficult. Many fundamental solutions bear the names of people who first obtained them (e.g. Kelvin fundamental solution, Melan fundamental solution, Rongved fundamental solution in elasticity, etc.).

The fundamental solutions of partial differential equations are generally formulated for infinite domains. In some cases, it is possible to find solutions to the governing differential equations for domains with additional boundaries or for finite domains knowing the conditions on some parts of these boundaries. In such cases, these solutions are called Green functions. There are several techniques to obtain Green's functions (the method of images, Fourier transforms, etc.) In most cases, Green's functions can only be found numerically.

Online Libraries

Other Online Sources

a) Theory

http://www.math.umn.edu/~olver/pd_/gf.pdf

http://mathworld.wolfram.com/GreensFunction.html

b) Mathematica™ introduction

http://www.nd.edu/~mjm/greens.func.pdf

c) Applications